The Parabola
The blue lines are perpendicular bisectors to the two points.
You can also make a parabola using the spreadsheet, see GeoGebra Tutorial - Spreadsheet.
The parabola is one of the conic sections, described by Apollonius in his book "Conics".
An ancient definition of a parabola is:
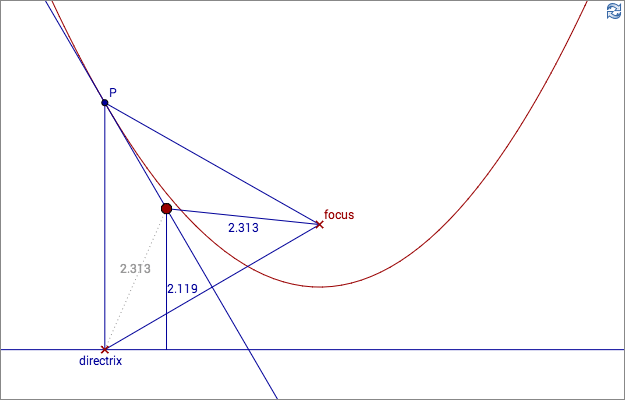
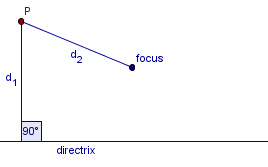
Given a line (a directrix) and a point (the focus point) find a point P with the distances (as in the picture) d1=d2. The parabola is the set of all such points.
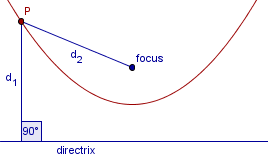
The point P lies on the perpendicular bisector. The perpendicular bisector intersects the parabola at one single point, the point P. It is hence a tangent line to the parabola.
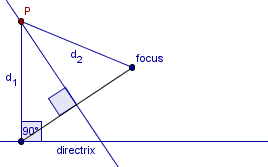
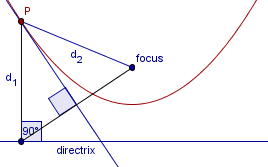
No other points on the perpendicular bisector lie on the parabola.
Exercise1
Place the focus on the y-axis at (0,a), the directrix at the x-axis, and let the point P have the coordinates (x,y). Find an expression for y in terms of x by using the distances d1=d2.
(Apollonius could not do this exercise, he wrote his books about 1800 years before the Cartesian plane was invented.)
The focus of a parabola
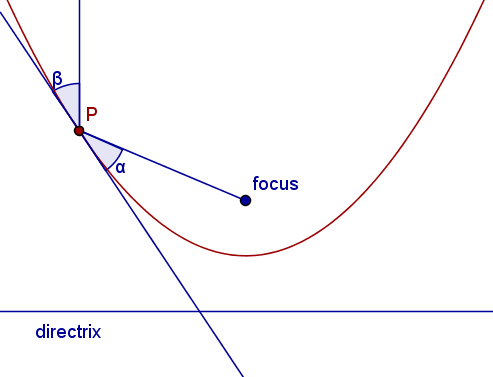
A ray falling onto a mirror will have a reflection such that:
the incident angle = the angle of reflection
Exercise 2
Show that a ray falling onto a parabola perpendicular to the directrix will be reflected to the focus point. In other words, show that α=β.
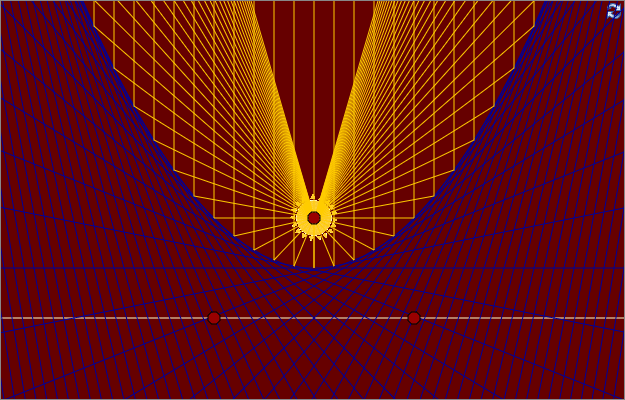
Other Conics
By letting the directrix being a circle instead of a line, you can get the shapes of the the other conics. Draw a perpendicular bisector between the focus point and a point on the circle.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License