Quadratic Functions
The most common way to write a quadratic function is to use general form:
\[f(x)=ax^2+bx+c\]
When analyzing the graph of a quadratic function, or the correspondence between the graph and solutions to quadratic equations, two other forms are more suitable: vertex form and factor form.
In order to rewrite a quadratic function from general form to vertex form, you must know how to complete the square.
Completing the square
Completing the square is a method used for solving quadratic equations and for rewriting quadratic functions to vertex form.
It is easy to solve a quadratic equation of the form \(x^2=c\), you just take the square root of both sides. You can also easily solve equations of the form \((ax+b)^2=c\), first take the square root of both sides, then solve for \(x\). When completing the square, you rewrite a quadratic equation to the form \((ax+b)^2=c\).
Let's say we want to solve an equation of the form
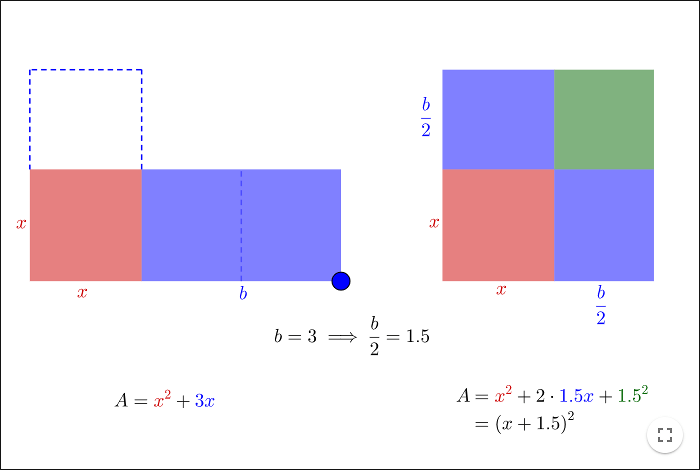
\[x^2+bx = a\]where both \(a\) and \(b\) are positive numbers. In this case, we can use areas to explain how to complete the square.
From the worksheet we get that
\[ \begin{align} x^2+bx &= a \\ x^2+bx + \left(\frac{b}{2}\right)^2 &= a + \left(\frac{b}{2}\right)^2 \\ \left(x+\frac{b}{2}\right)^2 &= a + \left(\frac{b}{2}\right)^2 \end{align} \]which is an equation we can solve.
It is possible to make a similar geometric construction for negative values of \(b\), but as long as we use a geometrical interpretation of the problem, \(a\) must not be negative and the geometrical solution will not yield negative \(x\)-values. In order to get all roots in the general case, it is better to use an algebraic approach.
The first person to find a method for solving quadratic functions was Brahmagupta, who also made one of the greatest contributions to mankind ever ‐ he showed how to do arithmetic calculations using the number zero.
Vertex form
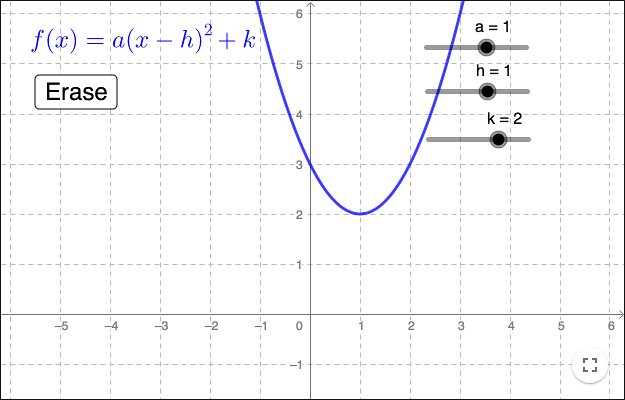
A quadratic function can always be written as
\[ f(x) = a(x-h)^2+k\]which is called vertex form.
What point is always on the graph regardless of the value of \(a\)?
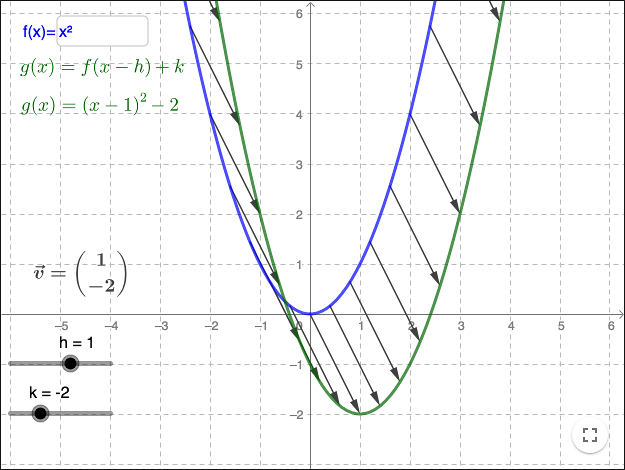
Translations of graphs
The graph of a quadratic function \(g(x)=(x-h)^2+k\), can be seen as the translation of the graph of the function \(f(x)=x^2\) along the vector
\[ \binom{h}{k}. \]From general form to vertex form
To rewrite a quadratic function from general to vertex form, you can complete the square. In the general we get this:
\[ \begin{align} f(x) &= ax^2+bx+c \\ &= a\left( x^2+\frac{b}{a}x+\frac{c}{a}\right) \\ &= a\left( x^2+2\frac{b}{2a}x+ \left(\frac{b}{2a} \right)^2-\left(\frac{b}{2a} \right)^2+\frac{c}{a}\right) \\ &= a\left( \left(x + \frac{b}{2a}\right)^2 -\left(\frac{b}{2a} \right)^2+\frac{c}{a}\right) \\ &= a\left(x + \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a} \end{align} \]Factor form
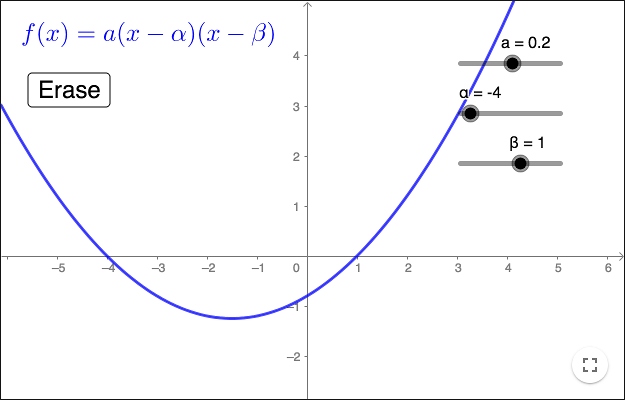
A quadratic function can always be written as
\[ f(x) = a(x-\alpha)(x-\beta\]which is called vertex form. The coefficients \(\alpha\) and \(\beta\) are roots to the quadratic equation \(f(x) = 0\).
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License