Limits

Limits as x tends to infinity

Intuitively we can understand that as \(x\) gets larger and larger, 1\(/x\) gets smaller and smaller. The limit of 1\(/x\) as \(x\) tends to infinity is zero. We write this as:

\[\lim_{x\rightarrow \infty}\frac{1}{x}=0\]

Note that an equality sign is used, the limit is equal to zero.

Another way of writing it is:

\[\frac{1}{x}\rightarrow 0 \text{ as } x\rightarrow \infty \]

Here we use arrows instead, 1\(/x\) is never equal to zero, but it tends to zero.

Do not mix "lim" and arrows, or expressions and equality-sign; choose one of the forms above!

In the general case we call the limit \(A\), and write it as

\[\lim_{x\rightarrow \infty}f(x)=A \]

The exact definition of a limit is not in the syllabus. Informally it means that the value of \(f(x)\) can be made as close to \(A\) as we want, if we just choose \(x\) large enough.

Horizontal asymptotes

If a function \(f(x)\) has the limit \(A\) as \(x\) tends to infinity, then the graph of \(f(x)\) will get closer and closer to the line \(y=A\). The line \(y=A\) is a horizontal asymptote to \(f(x)\).

Exercise 1

Graph following functions to find the horizontal asymptote (if there is one) as \(x\rightarrow \infty\).

1. \(\displaystyle{ f(x)=\frac{3x^3-x+1}{2x^3+2x^2} }\)
2. \(\displaystyle{ f(x)=\frac{1-2x}{1+2x} }\)
3. \(\displaystyle{ f(x)=\frac{1-2x}{1+2x^2} }\)
4. \(\displaystyle{f(x)=\frac{1+2x^2}{1+2x} }\)
5. \(\displaystyle{f(x)=\frac{x^2+x+1}{x^3+x^2+x+1} }\)
6. \(\displaystyle{f(x)=\frac{4x^4+x^3}{5x^4+x^2+1} }\)
7. \(\displaystyle{f(x)=2+\frac{\sin x}{x} }\)
8. \(\displaystyle{f(x)=2+\frac{x}{\sin x} }\)
9. \(\displaystyle{f(x)=2+\frac{x}{2+\sin x} }\)
10. \(\displaystyle{f(x)=2+\frac{1}{\sqrt{x}-100\cos x} }\)

Is there a way of finding the horizontal asymptote of a rational function (what’s a rational function?) without using an electronic device?

Can you figure out the limits 7-10 without plotting the graphs?

Limits as x tends to a

The function

\[f(x)=\frac{x^2+4x-12}{x^2-2x} \]

is not defined when \(x=2\), it does however have a limit as \(x\rightarrow 2\), the limit is \(4\). We write this as

\[\lim_{x\rightarrow 2}\frac{x^2+4x-12}{x^2-2x} = 4 \]

In this example it is easy to find the limit without graphing it

\[\lim_{x\rightarrow 2}\frac{x^2+4x-12}{x^2-2x} = \lim_{x\rightarrow 2} \frac{(x-2)(x+6)}{x(x-2)} = \lim_{x\rightarrow 2} \frac{x+6}{x} =\frac{2+6}{2}=4\]

Infinity as a limit, vertical asymptotes

The expression \(1/x^2\) gets larger and larger as \(x\) gets closer to zero. We write this as:

\[\lim_{x\rightarrow 0}\frac{1}{x^2}=\infty\]

Even though the notation above is often used, infinity is not usually seen as a limit since the infinity is not a number (unless you define it to be a number, see Extended real number line).

The graph of the function \(f(x)=1/x^2\) gets closer and closer to the line \(x=0\) as \(x\rightarrow 0\), the line \(x=0\) is a vertical asymptote.

Note that this is not true for general functions, see exercise 1 below.

Let

\[f(x)=\frac{x^2-3}{x^2+2x-8} \]

The denominator is zero when \(x=2\) and when \(x=-4\). The function has two vertical asymptotes.

We can approach the value \(x=2\) from two directions, either \(x\lt 2\) or \(2\lt x\) . In order for a limit to exist, the limits we get from the two directions must be the same. In this case a limit does not exist, not even infinity. The function does however have a vertical asymptote. Sometimes we want to specify that an expression has different limits depending on whether we approach the limit from the left or the right. We use a + (\(x\) is greater than) or a - (\(x\) is less then), to distinguish between the two cases.

\[\lim_{x\rightarrow 2^+} \frac{x^2-3}{x^2+2x-8} = \infty \]

\[\lim_{x\rightarrow 2^-} \frac{x^2-3}{x^2+2x-8} = -\infty \]

Difficult limits

In some cases you use common sense to find limits:

\[\frac{1}\infty = 0 \hspace{1 cm} \frac{1}{0}=\infty \hspace{1 cm} 1+\infty=\infty \hspace{1 cm} 2\cdot \infty = \infty\]

(Don't write like this on ↑ the exam)

It is difficult in some cases:

\[\frac{\infty}\infty = ? \hspace{1 cm} \frac{0}{0}=? \hspace{1 cm} \infty-\infty=? \hspace{1 cm} 0\cdot \infty = ?\]

Exercise 2

Graph the following functions to find the limits, if they exist.

1. \( \displaystyle{\lim_{x\rightarrow 0}\sin\left( \frac{1}{x}\right)} \)
2. \( \displaystyle{\lim_{x\rightarrow 0} x \cdot \sin\left( \frac{1}{x}\right)} \)
3. \( \displaystyle{\lim_{x\rightarrow 0} \frac{\sin x}{x} } \)
4. \( \displaystyle{\lim_{x\rightarrow 0} \frac{\cos x -1}{x} } \)

Sequences

A sequence is a function with the domain being the natural numbers \(\mathbb{N} \).

A sequence can be written like this \(a_0,a_1, a_2, \ldots \) or like this:

\[(a_n)_{n=0}^\infty \]

The limit of a sequence is written like this:

\[\lim_{n\rightarrow \infty}a_n=A \]

Exercise 3

Use a slider to represent \(n\).

Set the width of the slider to 500. Then find the limits, if they exist, of following sequences:

1. \(\displaystyle{\lim_{n \rightarrow \infty}1^n}\)
2. \(\displaystyle{\lim_{n \rightarrow \infty}0.99^n}\)
3. \(\displaystyle{\lim_{n \rightarrow \infty}1.01^n}\)
4. \(\displaystyle{\lim_{n \rightarrow \infty}\left( 1+\frac{1}{n}\right)}\)
5. \(\displaystyle{\lim_{n \rightarrow \infty}\left( 1+\frac{1}{n}\right)^n}\)

Limit of sin(x)/x, proof

It is easy to find the limit

\[\lim_{x \rightarrow 0}\frac{\sin x}{x} \]

numerically. If you want to prove what the limit is, you must use geometry.

In order for the limit to become an easy number, you must use radians for measuring angles, this is the reason why degrees are never used when doing calculus. This limit is used for finding the derivative of the trigonometric functions.

Load GeoGebra worksheet

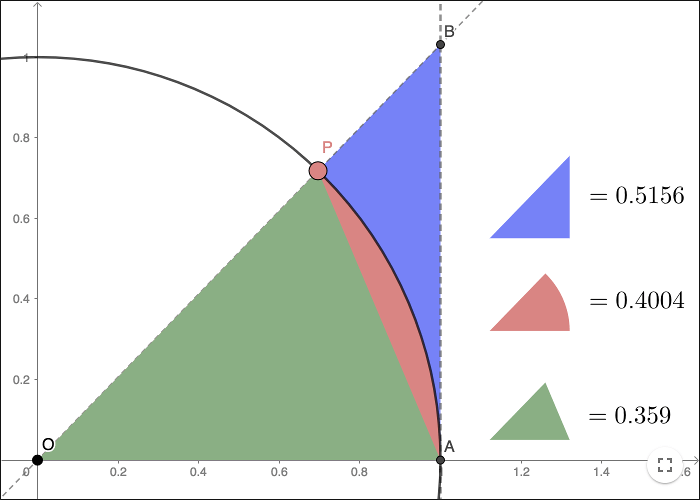
Exercise 4

Using the notations in the worksheet above:

Find the areas of the triangles \(\Delta OAP\), \(\Delta OAB\), and the area of the sector \( OAP \). Describe the areas in terms of \(\alpha \), \(\sin (\alpha)\) and \(\cos (\alpha)\).

Use the inequalities \(\Delta OAP \lt OAP \lt \Delta OAB \) to find the limit

\[\lim_{\alpha \rightarrow 0}\frac{\alpha}{\sin{\alpha}} \]

Rearrange the inequalities to find the limit

\[\lim_{\alpha \rightarrow 0}\frac{\sin \alpha }{\alpha} \]