The Definition of the Derivative

The derivative at a point

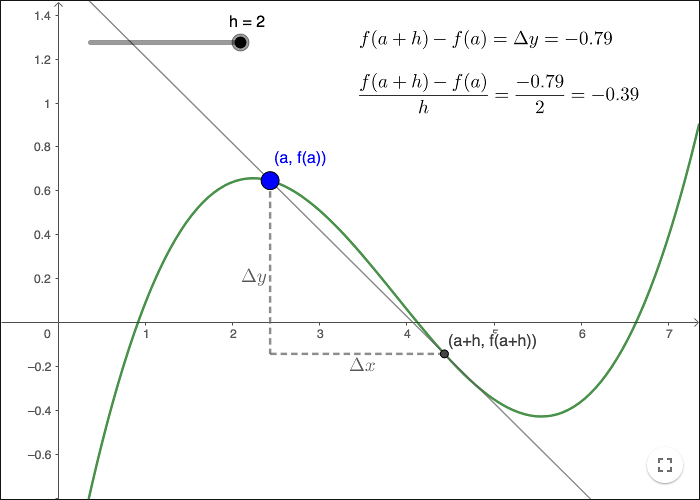
The derivative of a function \(f(x)\) at a point \( (a, f(a))\) is written as \(f'(a)\) and is defined as a limit.

\[f'(a)=\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\]

The value of

\[\frac{f(a+h)-f(a)}{h}\]

is the slope of the line through the points \( (a, f(a))\) and \( (a+h, f(a+h))\), the so called secant line.

Note that \(\Delta x = a+h-a=h\) and \(\Delta y = f(a+h)-f(a)\). The limit of the secant lines as \(h\) tends to zero is the tangent line. The derivative is the slope of the tangent line to the graph at the point where \(x=a\). Finding the derivative is called differentiating.

Load GeoGebra worksheet

Where on the graph is the derivative: positive, negative, zero? Does it matter if you approach the point from right or left, if h is positive or negative?

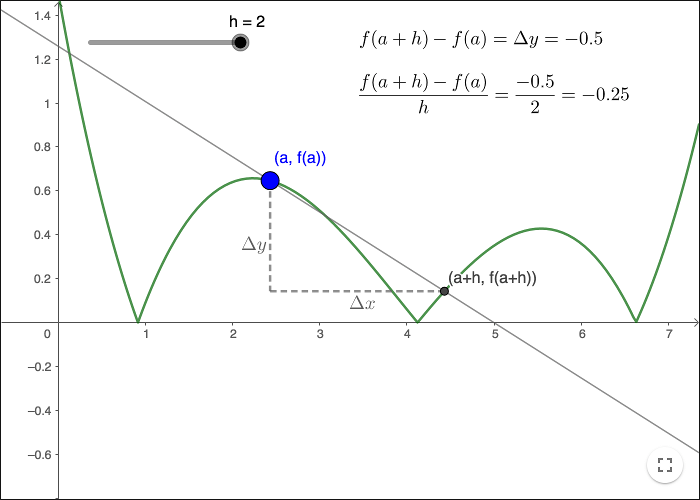
Taking the absolute value of the function above, you get the graph below.

Load GeoGebra worksheet

In the graph above: are there any points that makes defining the derivative difficult?

The derivative as a function

You can extend the definition of the derivative at a point to a definition concerning all points (all points where the derivative is defined, i.e. where the limit exists); if doing so you get a new function \(f'(x)\) defined like this:

\[f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} \]

Finding an algebraic formula for the derivative of a function by using the definition above, is sometimes called differentiating from first principle.

By using a computer you can find numerical approximations of the derivative at all points of the graph.

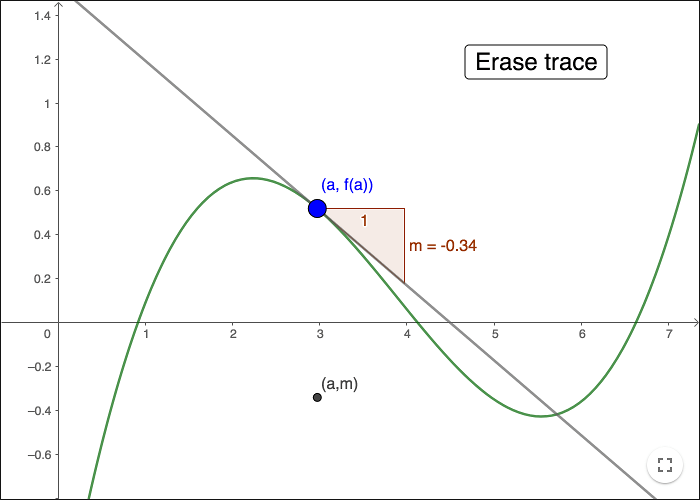
The line shown in the construction below is the tangent to the graph at the point A. The slope of the tangent line is the y-value of the point P. Drag the point A to see the trace of the point P, this trace is the graph of the derivative function.

Load GeoGebra worksheet

Try to change the constant term in the definition of the function to move the graph two units upward, i.e.

Note that the point P still has the same trace. There are infinitely many functions giving rise to the same derivative. These functions differ by a constant but their graphs have the "same shape".

Another way of writing it

If you instead use \(y\) to denote a function of a variable \(x\), \(y=f(x)\), then you use the notation \(\frac{dy}{dx}\) to denote the derivative. The notation stems from the definition

\[\frac{dy}{dx}=\lim_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}\]

Derivative of standard functions

You can algebraically find the derivative of all standard functions. Before doing so, we are going to explore some standard functions numerically.

Exercise 1

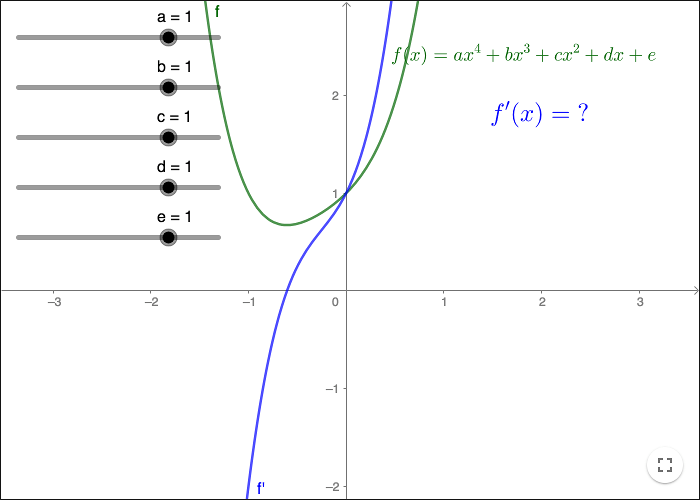
Polynomials

Load GeoGebra worksheet

• The constant function

  Let \(a=b=c=d=0\). Find a formula for \(f'(x)\)! Explain!

• First degree polynomials

  Let \(a=b=c=0\), try different values of \(d\). Find an exact formula for \(f'(x)\)! Explain!

  What happens with the graph of \(f'(x)\) when you change the slider \(e\)? Explain!

• Higher degree polynomials

  What kind of a function is \(f'(x)\) when \(f(x)\) is a second degree polynomial?

  What kind of a function is \(f'(x)\) when \(f(x)\) is a third degree polynomial? Make a guess!

  What kind of a function is \(f'(x)\) when \(f(x)\) is a fourth degree polynomial? Make a guess!

  What happens with the graph of \(f'(x)\) when you change the slider e?

• The derivative of a polynomial of degree \(n\)

  Try to find an exact formula for \(f'(x)\) when \(f(x)=cx^2\) (let the sliders \(a, b, d, e\) be zero). How is the gradient of the line related to the number \(c\)? Try to figure it out by changing the slider c.

  Having the formulae for \(f'(x)\) when \(f(x)=ax^0, f(x)=ax^1, f(x)=ax^2\); try to guess the formula for \(f'(x)\) when \(f(x)=ax^3\) and \(f(x)=ax^4\).

• Antiderivative

  If \(f'(x)=3\) what is \(f(x)\)? Could many functions have the same derivative functions?

  If \(f'(x)=4x\) what is \(f(x)\)?

  If \(f'(x)=6x^2\) what is \(f(x)\)?

  If \(f'(x)=x^{-1}\) what is \(f(x)\)?

Exercise 2

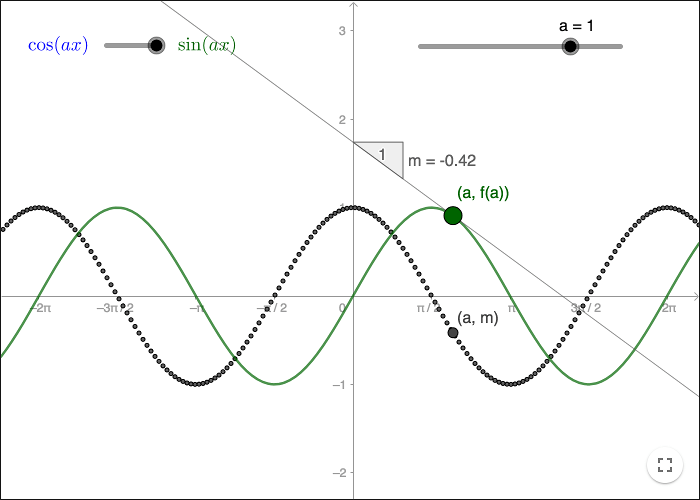
Sine and cosine

Load GeoGebra worksheet

Guess the derivative function of \(f(x)=\sin (ax)\) when \(a=1\).

Guess the derivative function of \(f(x)=\sin (ax)\) when \(a\neq 1\).

Change to the function \(f(x)=\cos (ax)\) by changing the left slider. Guess the derivative function of \(f(x)=\cos (ax)\) when \(a=1\).

Guess the derivative function of \(f(x)=\cos (ax)\) when \(a\neq 1\).

Exercise 3

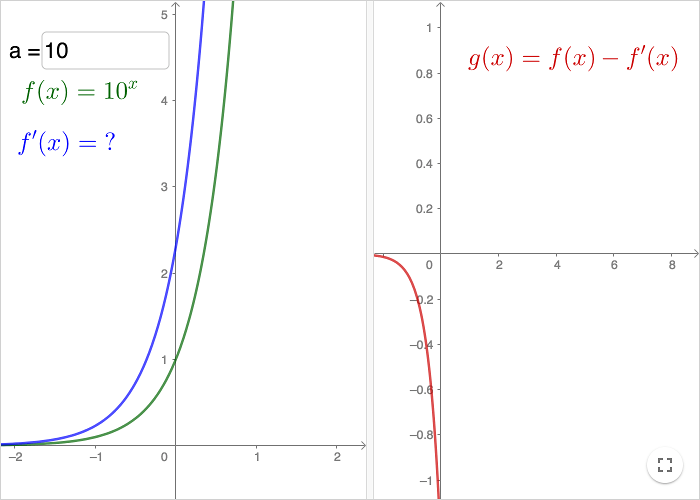
Exponential function

Load GeoGebra worksheet

To the left in the workseet above, the graph of the function \(f(x)=a^x\) and its derivative function is shown. To right the difference between these two functions is shown.

Change the base of the exponential function by entering a new value of \(a\) in the input box.

Find a value of the base that makes the two functions as close as possible, the value should be correct to four significant figures.

Exercise 4

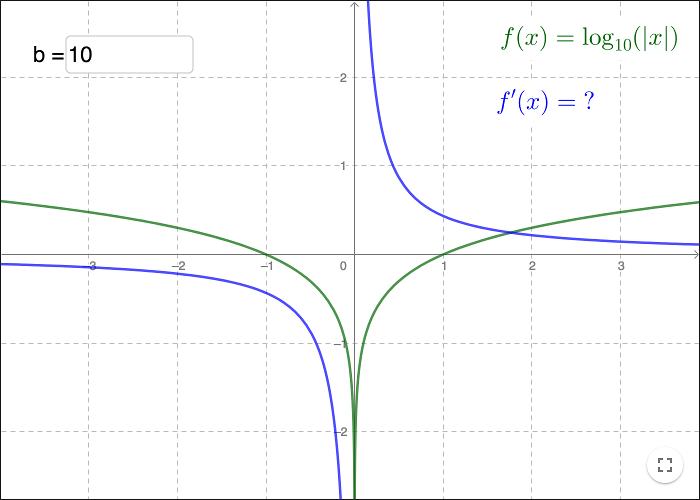
Logarithmic function using a convenient base

Load GeoGebra worksheet

Try to find a base \(b\) such that the derivative is \(\frac{1}{x}\).