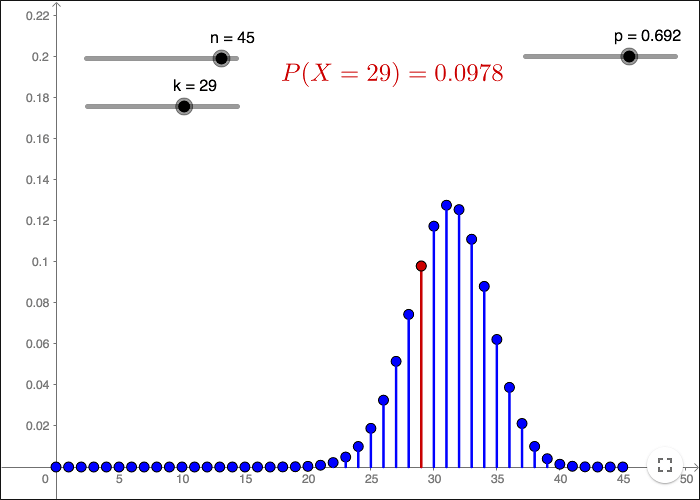
Binomial Distribution
In a Bernoulli trial the outcome can be either "success" or "failure". If \(p\) denotes the probability of success then the probability of failure is \(1-p\). When doing \(n\) trials the probability of getting exactly \(k\) successes is given by
\[P\;(X=x)=\binom{n}{k}p^k(1-p)^{n-k}\]
where \(X\) is a binomially distributed random variable. We use the notation: \(X\sim B(n,p)\).
Mean and variance for binomial distribution
The mean of one trial is given by \(\mu = 1\cdot p+0\cdot (1-p)=p\). The mean of \(n\) independent trials is hence \(\mu = np\).
The variance of one trial is given by
\[\sigma^2=(1-\mu)^2\cdot p + (0-\mu)^2\cdot (1-p)= (1-p)^2\cdot p + p^2\cdot (1-p)=p\cdot (1-p) \]
The variance of \(n\) independent trials is hence \(\sigma^2=np(1-p)\).
\[\mu = np \hspace{1cm} \sigma^2=np(1-p) \]
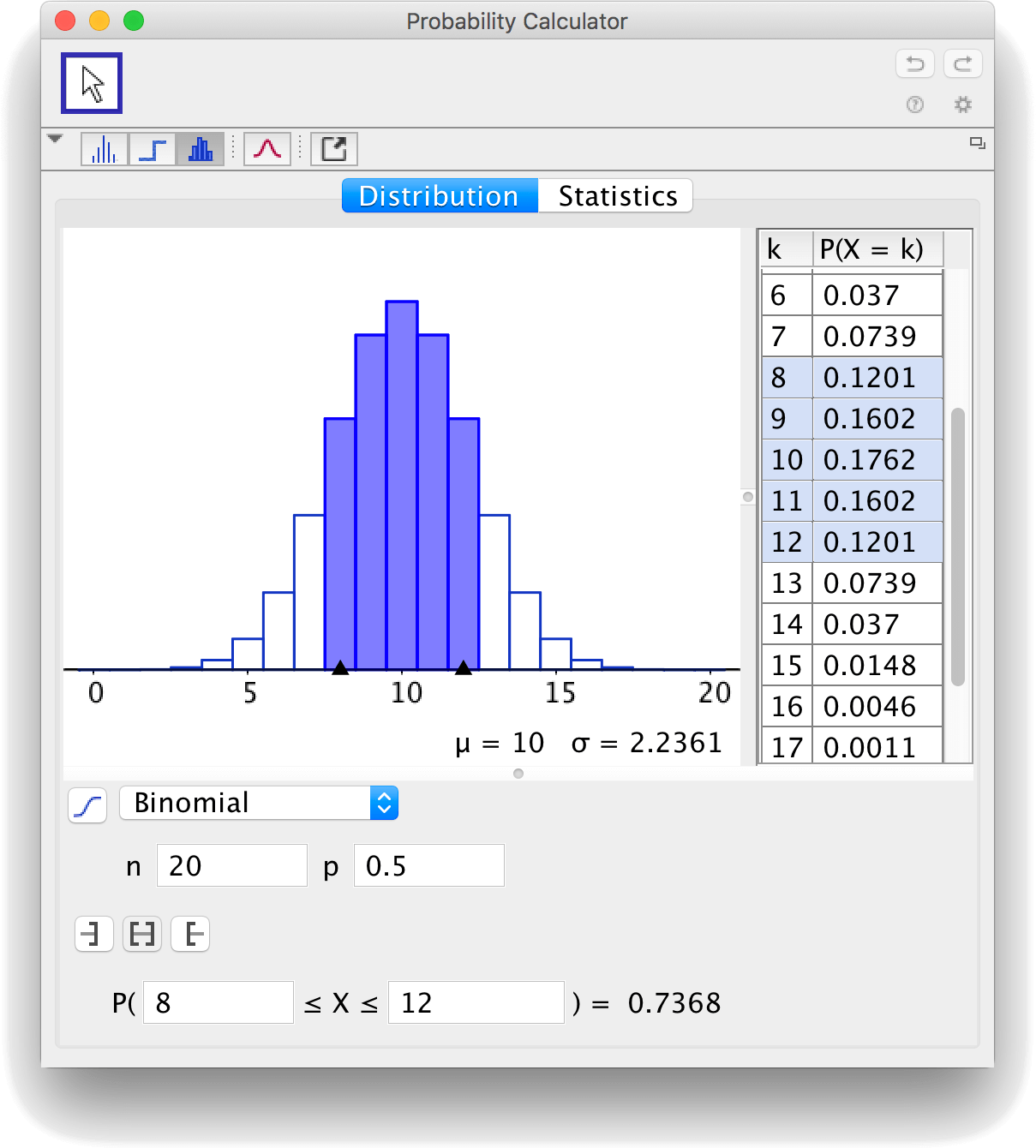
Binomial distribution in GeoGebra
By using the tool
Probability Calculator,
you can find all probabilities for a binomial distribution. The tool is found in the menu belonging to the spreadsheet.
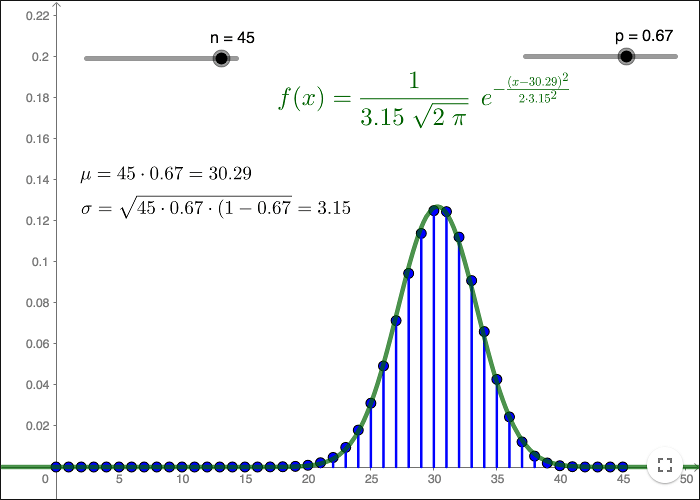
Binomial and normal distribution
Using the mean \(\mu = np\) and the variance \(\sigma^2=np(1-p)\) of the binomial distribution as parameters in the function describing the normal pdf
\[f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{\left( - \dfrac{(x-\mu)^2}{2\sigma^2}\right)} \]
we get a continuous approximation of the binomial distribution. When \(n\) is large and when \(p\) is not too close to 0 or 1, the normal distribution is a very good approximation of the binomial distribution.
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License