Basic Code
Special keys
Many script-languages use backslash "\" to denote special commands. In LaTeX backslash is used to generate a special symbol or a command.
Curly brackets are used to group characters.
Hat and underscore are used for superscripts and subscripts.
Superscripts, subscripts and groups of characters
| Formula | LaTeX-code |
|---|---|
| \(x^2\) | x^2 |
| \(x^{2+a} \) | x^{2+a} |
| \(n_1 \) | n_1 |
| \(n_{k+1} \) | n_{k+1} |
| \(n_{k+1}^2 \) | n_{k+1}^2 |
| \(e^{e^{e^{e^{x}}}} \) | e^{e^{e^{e^{x}}}} |
Arithmetics
By convention you should either not write a multiplication-sign at all, as in \(y=mx+c\);
or you should write it using a vertically centered dot, as in \(3\cdot5=15\). Do not use symbols like
"*"! In LaTeX you use the command \cdot to make a multiplication-dot.
Sometimes you can use the symbol \(\times\). A matrix having \(n\) rows and \(m\) columns
is a \(m\times n\)-matrix. The code \times is used in LaTeX to make the symbol \(\times\).
The square root symbol is written using the command \sqrt{expression}. The \(n\)-th root is written
using the command \sqrt[n]{expression}.
The square root of a number can never be negative by definition. The root of a quadratic equation however, can be either
positive or negative. The solution to the equation \(x^2=4\) is given by \(x = \pm 2\). The symbol
\(\pm\) is written using the code \pm in LaTeX.
To write a fraction, you use the code \frac{expression in the numerator}{expression in the denominator}.
Formulas that appear in text are called inline. Inline formulas are sometimes squashed to avoid altering the height
of the lines. Squashed fractions may look strange, and for that reason there is a special command to force a fraction to appear as
displaystyle even though it is inline; the command is \dfrac.
\frac{2}{3}. This is an inline fraction in displaystyle \(\dfrac{2}{3}\), written using the code
\dfrac{2}{3}.
| Formula | LaTeX-code |
|---|---|
| \(3\cdot5=15 \) | 3\cdot5=15 |
| \(n\times m \) | n\times m |
| \(\pm 2 \) | \pm 2 |
| \(2\div 3 \) | 2\div 3 |
| \(\frac{2}{3} \) | \frac{2}{3} |
| \(\sqrt{2} \) | \sqrt{2} |
| \(\sqrt[3]{8}=8^{\frac{1}{3}}=2 \) | \sqrt[3]{8}=8^{\frac{1}{3}}=2 |
| \(\frac{2/3}{4/5} \) | \frac{2/3}{4/5} |
| \(\frac{\frac{2}{3}}{\frac{4}{5}} \) | \frac{\frac{2}{3}}{\frac{4}{5}} |
| \(\frac{\dfrac{2}{3}}{\dfrac{4}{5}} \) | \frac{\dfrac{2}{3}}{\dfrac{4}{5}} |
Standard functions
By convention, variables are written in italics. For that reason all text when writing in math mode is in italics. In some cases however, the text should not be in italics. One such example is the mathematical standard functions.
| Formula | LaTeX-code |
|---|---|
| \(lne^x = x \) (wrong by convention) | lne^x = x |
| \(\ln e^x = x \) (correct by convention) | \ln e^x = x (note the space after \ln) |
There are commands for all standard functions; here are some examples:
\sin \cos \tan \arcsin \arccos \arctan \ln \log
Text in math mode
Sometimes you need text that isn't written in italics even though it's written in math mode.
| Formula | LaTeX-code |
|---|---|
| \( 3\text{ apples}\times 5\text{ apples} \) | 3\text{ apples}\times 5\text{ apples} |
Brackets
Since mathematical expressions often vary in height, you sometimes need brackets of varying heights. You can specify
a bracket by labelling the left bracket and the right bracket, then LaTeX will find the height of the expression
enclosed by those brackets and adjust the heights of the brackets accordingly. You specify the brackets by using
the commands \left and \right. Note that you need both commands, otherwise there is no
way for the program to determine the height of the expression. Sometimes you may need only one bracket that is
adjusted to the height of an expression; in such a case you can use an invisible bracket at one of the sides.
You make an invisible bracket by adding a point, i.e. by using the command \left..
Some brackets are written using regular keyboard strokes, such as these: (), [], ||.
| is written by using option+7 on a Mac, and Alt Gr+< on Windows/Linux. How to write various special characters using a Mac, is shown here.
Other brackets, on the other hand, have special meaning in LaTeX-code; you can't just write { since this character is used for grouping characters. If you want to write such a bracket, you must escape it using a backslash in front of it.
| Formula | LaTeX-code |
|---|---|
| \( (1+\frac{1}{x})^2 \) | (1+\frac{1}{x})^2 |
| \( \left(1+\frac{1}{x}\right)^2 \) | \left(1+\frac{1}{x}\right)^2 |
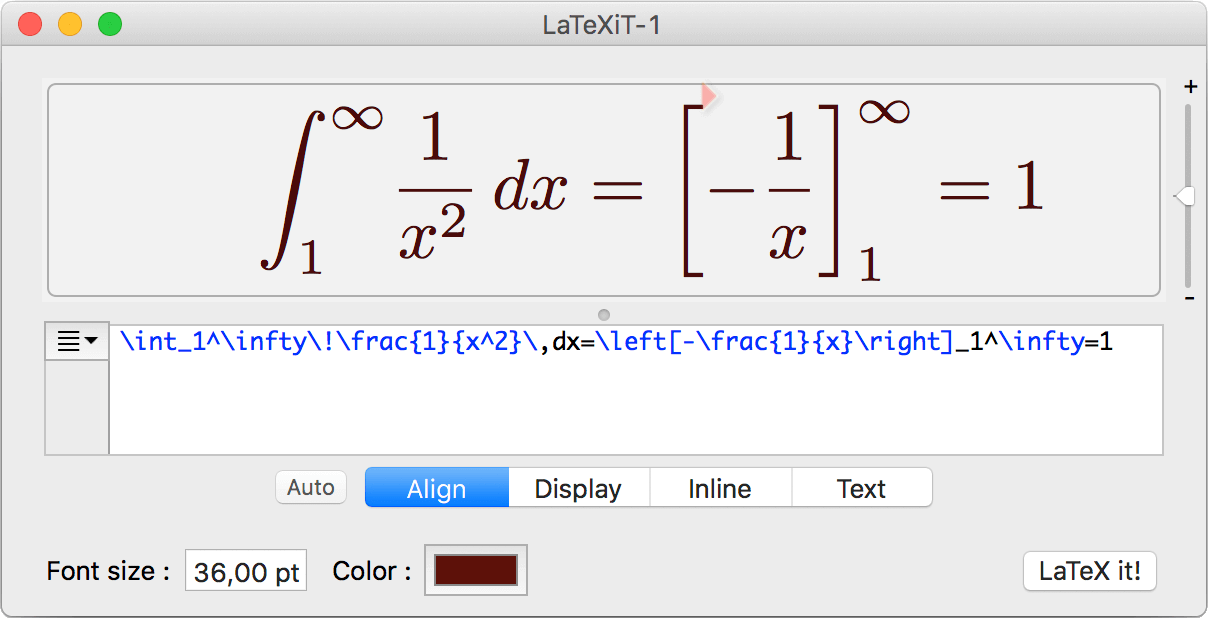
| \( \left[-\frac{1}{x}\right]_1^\infty \) | \left[-\frac{1}{x}\right]_1^\infty |
| \( \{1,2,3,\ldots ,n\}\) | \{1,2,3,\ldots ,n\} |
| \( \left\{1,\frac{1}{2},\frac{1}{3},\ldots ,\frac{1}{n}\right\} \) | \left\{1,\frac{1}{2},\frac{1}{3},\ldots ,\frac{1}{n}\right\} |
| \( \left.\frac{1}{1+x^2}\right|_0^\infty \) | \left.\frac{1}{1+x^2}\right|_0^\infty |
Integrals, series and limits
When writing integrals, series using sigma-notation or limits; you often want to specify boundaries. You use the same characters as are used for subscripts and superscripts when specifying boundaries.
When it comes the integrals, the boundaries are placed beside the integral-sign. In some cases you may want to
place the boundary below the integral-sign; you can then use the command \limits_{}.
The commands used are \int for integral, \sum for sigma-notation, \lim
for limits and \prod products.
| Formula | LaTeX-code |
|---|---|
| \( \int_0^2x^2dx \) | \int_0^2x^2dx |
| \( \int\limits_{x\in C}dx \) | \int\limits_{x\in C}dx |
| \( \sum_{i=1}^{n}i=\frac{n(n+1)}{2} \) | \sum_{i=1}^{n}i=\frac{n(n+1)}{2} |
| \( \lim_{h\to 0}\frac{f(x+h)-f(x)}{h} \) | \lim_{h\to 0}\frac{f(x+h)-f(x)}{h} |
| \( \prod_{i=1}^ni=n! \) | \prod_{i=1}^ni=n! |
Using display it looks like this:
\[ \begin{align*} &\int_0^2x^2dx \\ & \int\limits_{x\in C}dx \\ & \sum_{i=1}^{n}i=\frac{n(n+1)}{2} \\ & \lim_{h\to 0}\frac{f(x+h)-f(x)}{h} \\ & \prod_{i=1}^ni=n! \end{align*} \]Spaces
In math mode you don't get a space when using space bar, white spaces are simply ignored. If you need a space, there
are three commands; \, for a short space, \: for a medium space and \;
for a long space. If you want to reduce the space between two characters, you use the command \!;
this command is useful for reducing the space between the integral-sign and the integrand.
| Formula | LaTeX-code |
|---|---|
| \( a b \) | a b |
| \( a\: b \) | a\: b |
| \( \int\limits_{x\in C}xdx \) | \int\limits_{x\in C}xdx |
| \( \int\limits_{x\in C}\! x\, dx \) | \int\limits_{x\in C}\! x\, dx |
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License