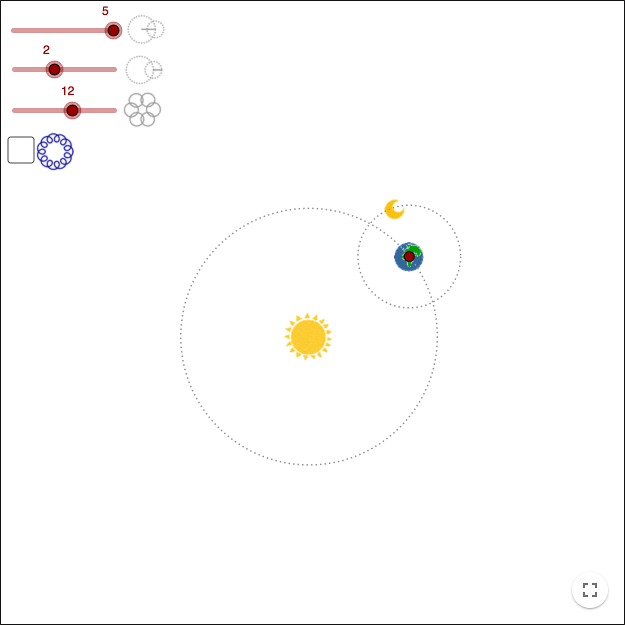
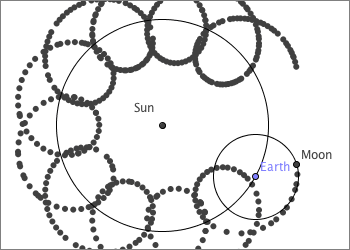
Sun, earth and moon

Load GeoGebra worksheet

Move the earth by dragging the red point. Check the check box to view the path of the moon. Change the radius of the earth and the radius of the moon. Change the number of months in a year.

Create epicycles without trigonometry

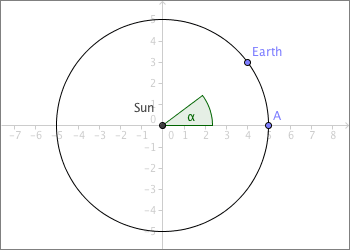
• Place a point Sun at the origin.
• Enter a circle having constant radius and the point Sun as centre. Use the tool Circle with Center and Radius.
• Insert a point Earth on the circle.
• Make a point A on the circle, make sure A lies on the x-axes; then measure the angle α, as in the picture.

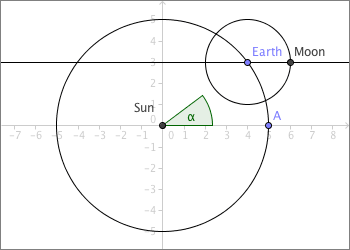
• Make a circle having constant radius and the point Earth as centre.
• Make a line through Earth parallel to the x-axes, then make the intersection point between the circle and the line. Name the intersection point Moon.
• You can not move the point Moon since it is an intersection point. This is not the point that is going to represent the moon.

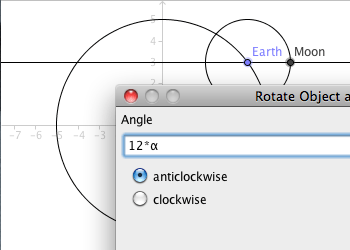
• There are 12 months in a year. Every time the earth makes one revolution around the sun, the moon has to make 12 revolutions around the earth. The angle the moon has to the x-axes should hence be 12 times the angle of the earth, i.e. the angle α.
• Rotate the point Moon around the point Earth by using the tool Rotate around Point.
• When you enter the angle, enter 12*α.

• The rotated point Moon', is the point representing the moon. Rename it to Moon (the other point will automatically be renamed, two objects must not share the same name).
• Hide all objects that should not be shown. Right-click on Moon and choose Trace on. You can now show the path of the moon as the earth moves by dragging the earth.
• Right-click on the earth and choose "Animation On".

You can vary the radii of the two circles by using sliders instead of constant numbers. You can also vary the number of months in a year by using a slider instead of the number 12 when rotating the moon. As a final touch you use images instead of points.

The pattern made by the moon, is the same kind of pattern you can get from a spirograph. To see more spirograph patterns, see Trigonometry - Epitrochoids and Hypotrochoids.