Trigonometric Laws
A standard way of denoting sides and angles in a triangle, is to denote the angles \(A,B,C\) (just as the vertices in GeoGebra). Then denote the side opposite of an angle with the same letter as the angle but use lower case.
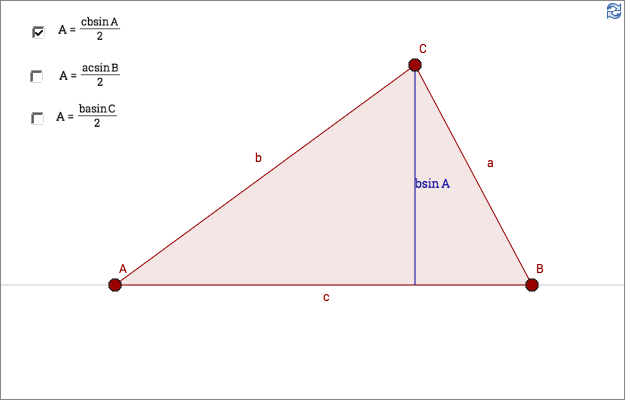
Triangle area using sine
If you know two sides of a triangle and the angle between those two sides, you can use the area law that uses sine.
\[A=\frac{bc\sin A}{2}=\frac{ac\sin B}{2}=\frac{ab\sin C}{2}\]
Law of sines
Using the area law, one can deduce following equalities:
\[b\sin A = a\sin B \hspace{1cm} c\sin B = b\sin C \hspace{1cm} c\sin A =a \sin C \]
After rearrangements, this can be written as the law of sines in two different ways.
\[\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\]
or
\[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\]
Law of cosines
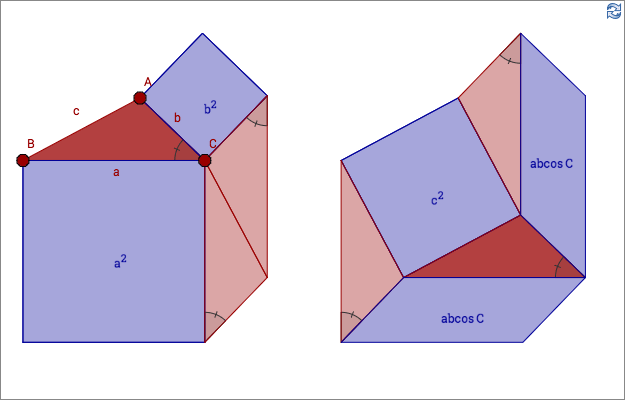
In the applet above, the red triangles are congruent. The blue area in each heptagon (polygon with seven vertices), is the remaining area when the area of the three triangles is subtracted from the area of the heptagon. Hence, the blue area of the two heptagons are the same, yielding:
\[a^2+b^2=c^2+2ab\cos C\]
The areas of the parallelograms are explained by the picture below.
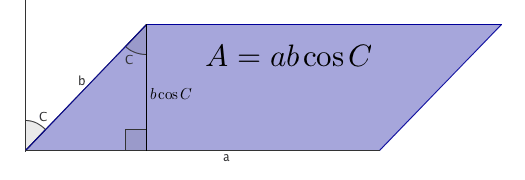
By dragging the point A to make a right-angled triangle, one can see that Pythagoras' theorem is a special case of the law of cosine.
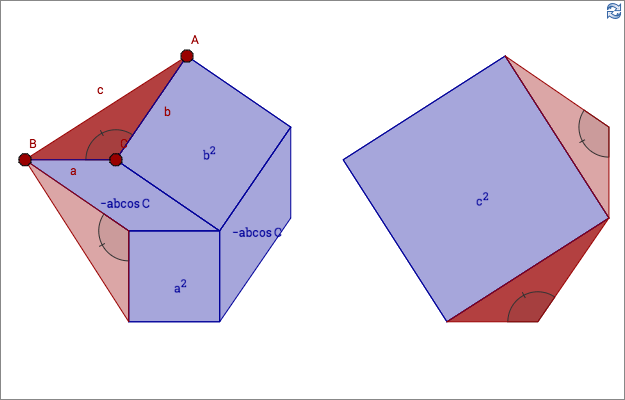
In the applet above, the triangle is acute (all angles are acute). In the applet below, the triangle is obtuse (one angle is obtuse).
The areas of the parallelograms are explained by the picture below.
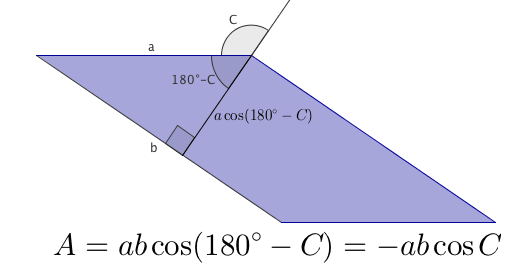
From symmetry, we get three cases of the law of cosines.
\[c^2=a^2+b^2-2ab\cos C\]
or
\[b^2=a^2+c^2-2ac\cos B\]
or
\[a^2=b^2+c^2-2bc\cos A\]
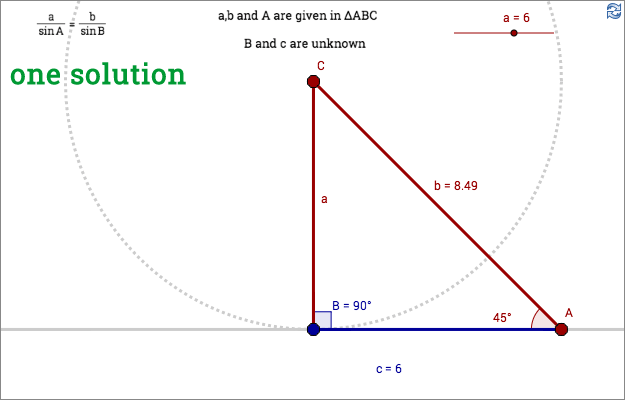
The ambiguous case
Using the laws of sines or cosines, one can find an unknown side or angle in a triangle.
In some cases there are two possibilities for the unknown side/angle. In the applet below, this is shown using law of sines. The same situation appears as two solutions to a quadratic equation when using law of cosines.
reference:
Geometric proof of law of cosines from Wikipedia - Law of cosines
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License