Multiply Fractions
Unit fractions
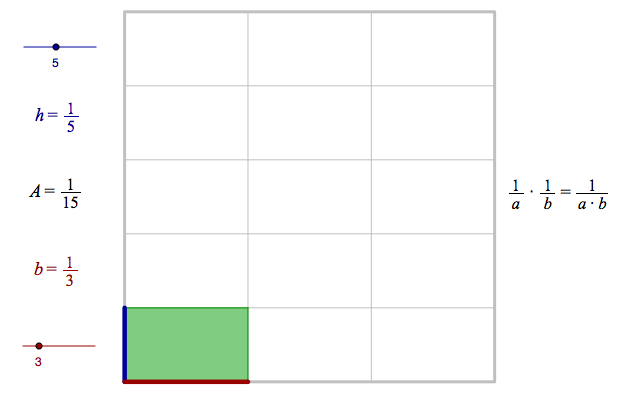
Fractions whose numerator is one, are called unit fractions. If you want to find the area of a rectangle with sides that are unit fractions, you can divide a unit square into small rectangles.
If the height is 1/5, the square must be divided into five pieces along the height. If the base is 1/3, the square must be divided into three pieces along the base. All in all you get 15 small rectangles. The area of the original rectangle is hence 1/15.
General fractions
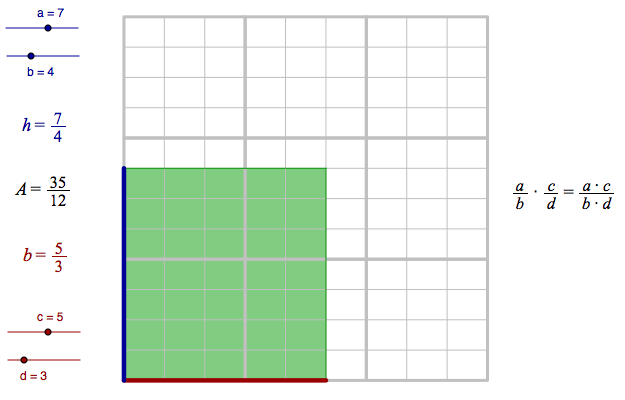
In the general case, the denominators will divide a unit square into smaller rectangles. By multiplying the numerators, you find how many of these small rectangles the original rectangle is made of.
In the real general case, the sides of a rectangle might be irrational numbers. Finding the area of the rectangle in this case is just a tad more complicated; the result, however, is still the base times the height.
further info:
in ancient Egypt they could only handle unit fractions:
http://en.wikipedia.org/wiki/Egyptian_fraction
irrational numbers: http://en.wikipedia.org/wiki/Irrational_number
irrational numbers on YouTube: http://www.youtube.com/watch?v=oORCAz-V_Bg
Platonic Realms Minitexts: What is..."How many?"
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License