Polynom
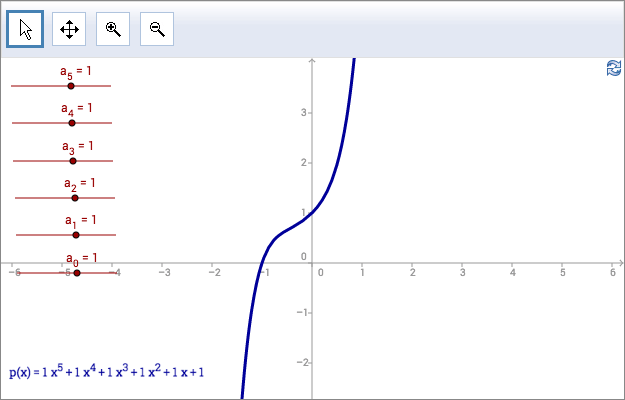
Ett allmänt polynom \(p(x)\) av grad \(n\) kan skrivas
\[p(x)=a_nx^n+a_{n-1}x^{n-1}+ \ldots +a_2x^2+a_1x+a_0\]
där \(a_n\neq 0\). Talen \(a_n\) kallas koefficienter.
En kvadratisk funktion är ett polynom av grad två. En kvadratisk funktion har en lokal extrempunkt, dvs en punkt där den har antingen ett lokalt maximum eller lokalt minimum. Använd appleten ovan för att bestämma hur många lokala extrempunkter ett femtegradspolynom kan ha. Låt \(a_5=0\) och bestäm hur många lokala extrempunkter ett fjärdegradspolynom kan ha. Hur många lokala extrempunkter kan ett tredjegradspolynom ha?
Övningar
Övning 1 - Kvadratisk funktion och linje
Vilken slutsats kan du dra av appleten nedan? Bevisa din slutsats!
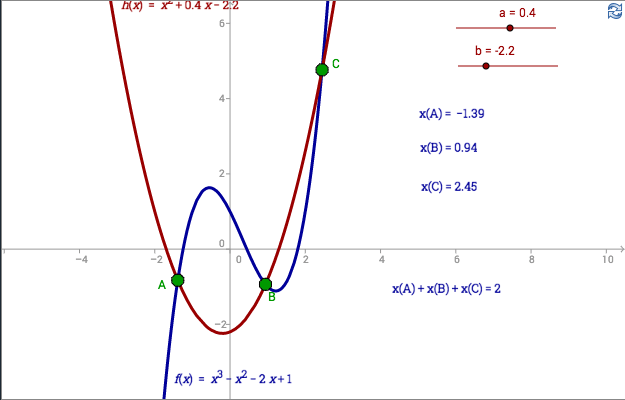
Övning 2 - Tredjegrads- och andragradspolynom
Vilken slutsats kan du dra av appleten nedan? Bevisa din slutsats!
mer info:
Idé om kvadratisk funktion och linje från pluttifikasjonparabel av Oisteing
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License