Polynomials
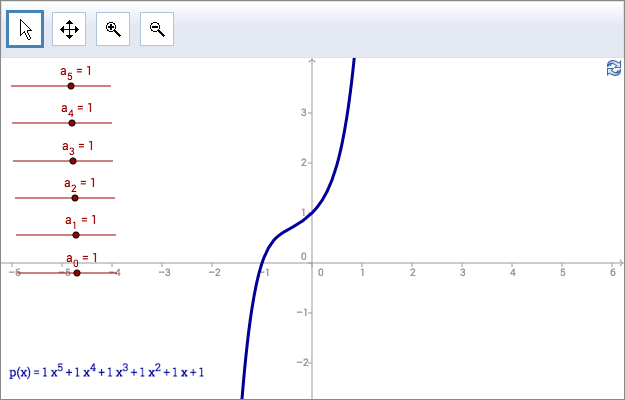
A general polynomial \(p(x)\) of degree \(n\) can be written
\[p(x)=a_nx^n+a_{n-1}x^{n-1}+ \ldots +a_2x^2+a_1x+a_0\]
where \(a_n\neq 0\). The numbers \(a_n\) are called coefficients.
A quadratic function is a polynomial of degree two, it has one turning point. Use the applet above to find how many turning points a polynomial of degree five can have. By letting \(a_5=0\), find how many turning points a polynomial of degree four can have. How many turning points can a polynomial of degree three have?
Exercises
Exercise 1 - Quadratic and Line
What conclusion can you make using the applet below. Prove that your observation is always correct.
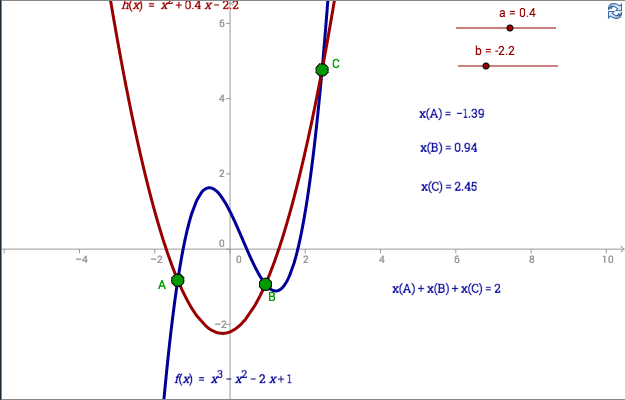
Exercise 2 - Cubic and Quadratic
What conclusion can you make using the applet below. Prove that your observation is always correct.
further info:
Quadratic-and-line-idea from pluttifikasjonparabel by Oisteing
by Malin Christersson under a Creative Commons Attribution-Noncommercial-Share Alike 2.5 Sweden License